BSpline 三次B样条曲线

BSpline 三次B样条曲线简介与推导

BSpline 三次B样条曲线

B样条

$$P(u)=\sum_{i=0}^n P_i B_{i,k}(u) \quad u\in[u_{k-1},u_{n+1}]$$

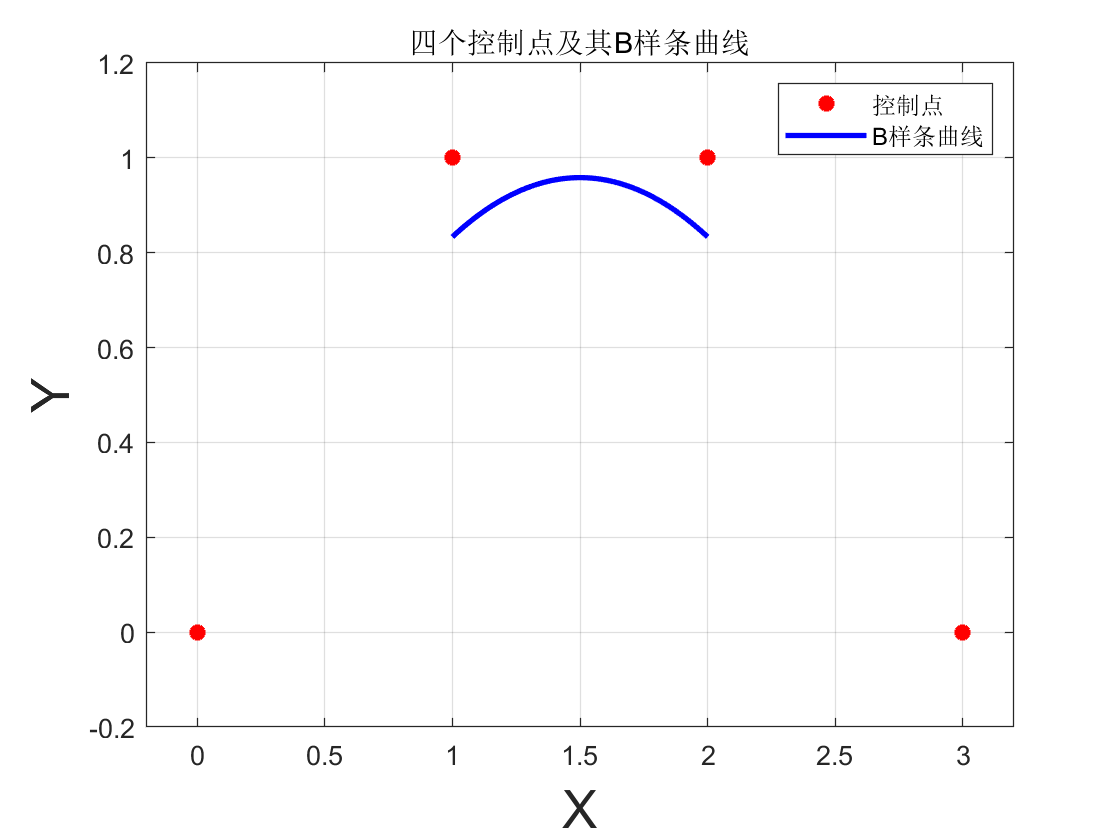
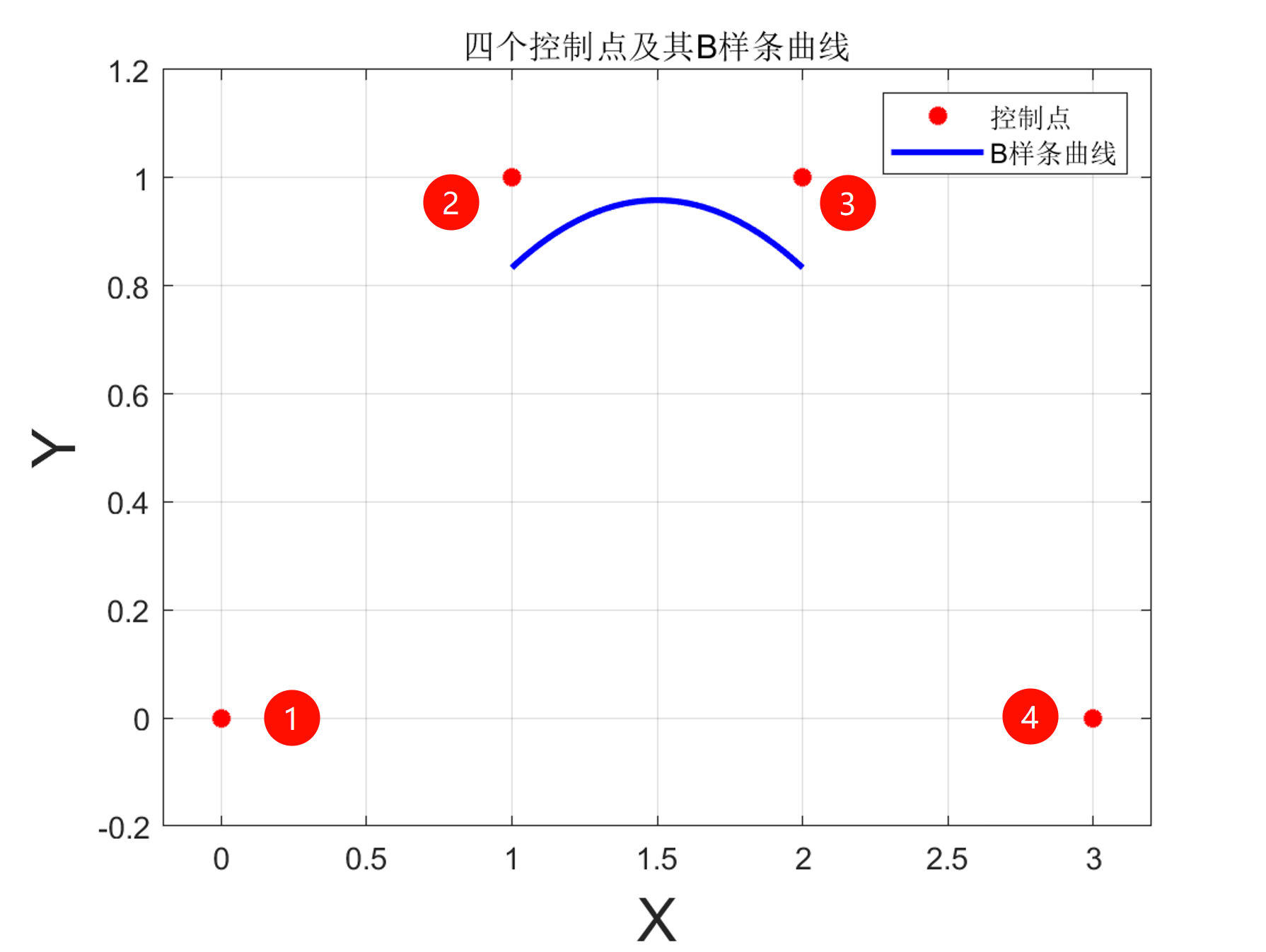
四点三次B样条曲线

$$P(s)=f_1(s)C_1+f_2(s)C_2+f_3(s)C_3+f_4(s)C_4$$

四个样条函数（基函数）

\begin{align} f_1(s)&=\frac{1}{6}(-s^3+3s^2-3s+1) \\ f_2(s)&=\frac{1}{6}(3s^3-6s^2+4) \\ f_3(s)&=\frac{1}{6}(-3s^3+3s^2+3s+1) \\ f_4(s)&=\frac{1}{6}s^3 \end{align}

其中：

$s$为归一化路径：$0\leq s\leq 1$

超过四个点？

如果超过了四个点位，我们是否要用更高次幂的函数来拟合？

这样会需要更复杂的运算，并且会导致牵一发而动全身的缺点，无法进行局部调整

当然，也有这种曲线，就是贝塞尔曲线（Bézier Curves）

贝塞尔曲线

Photoshop中三阶贝塞尔曲线

四点三阶B样条

也就是：

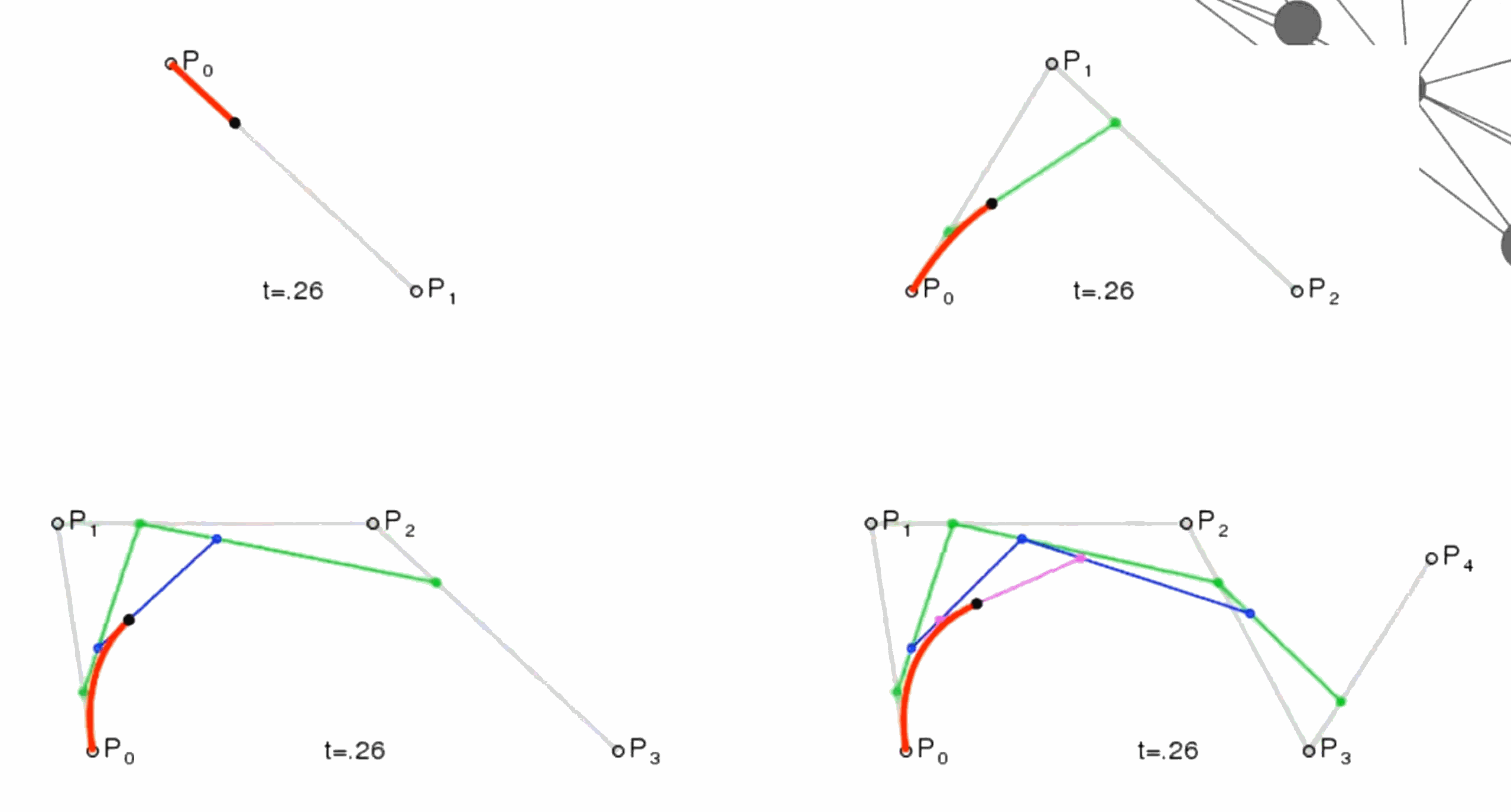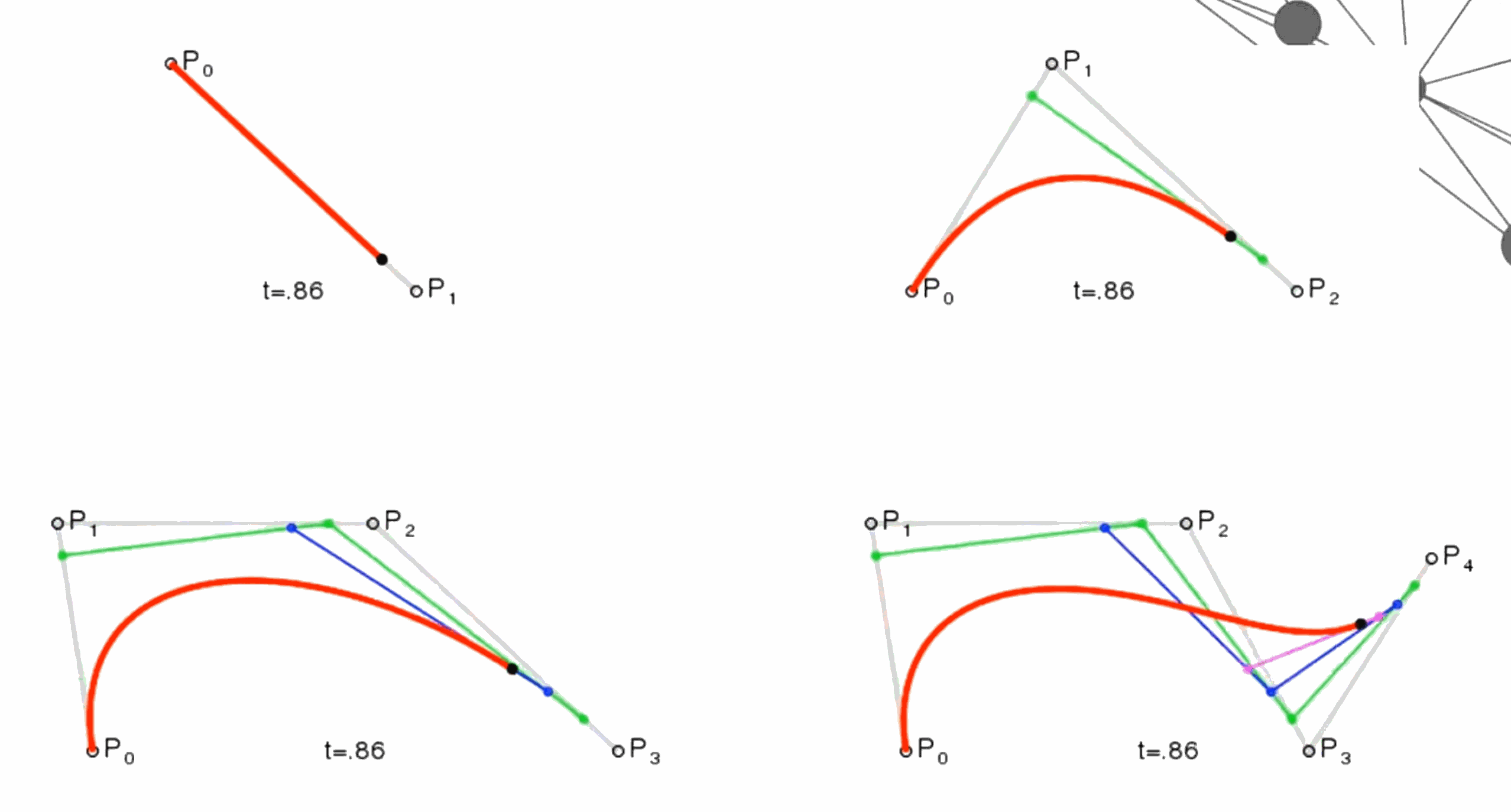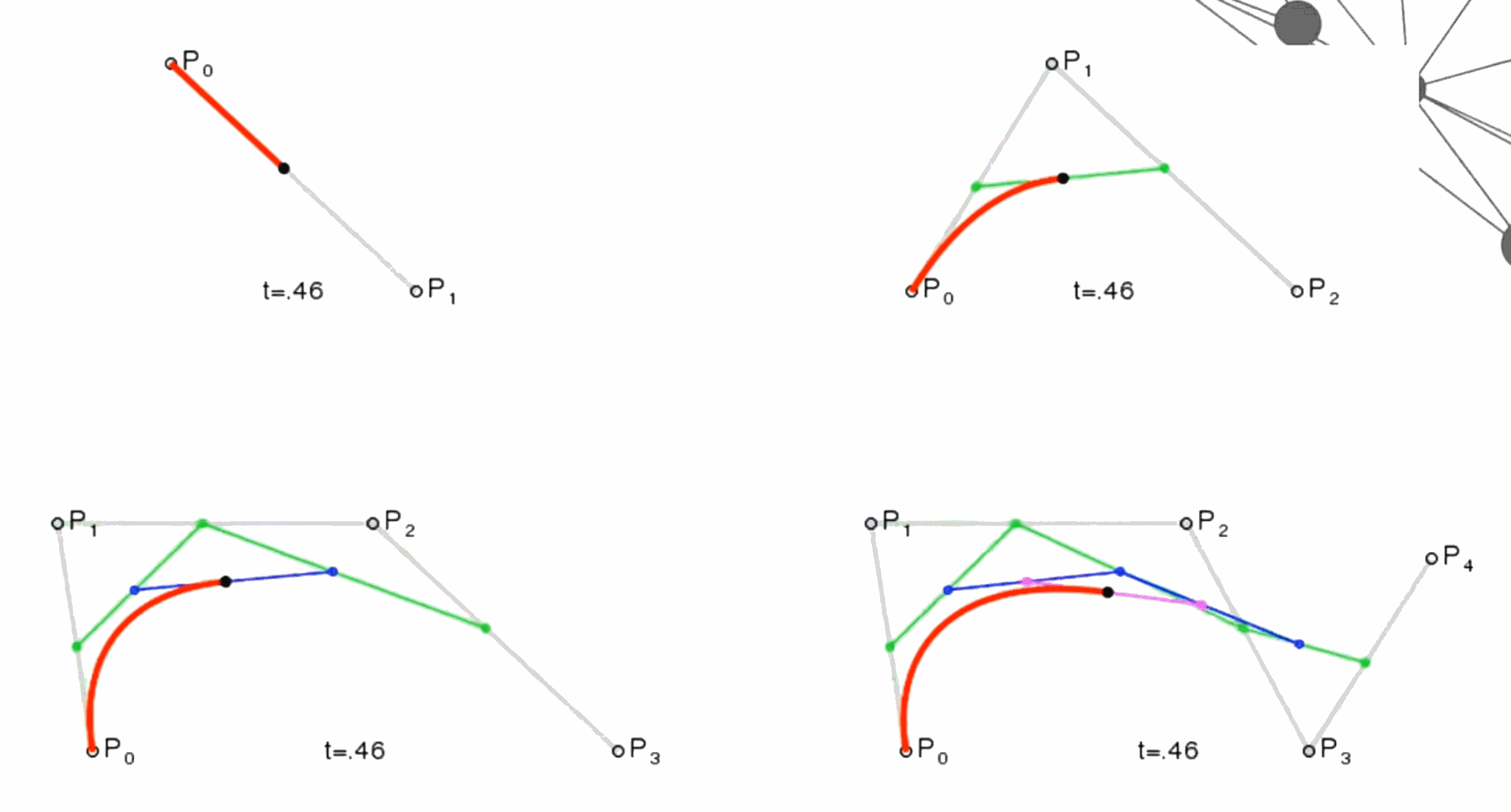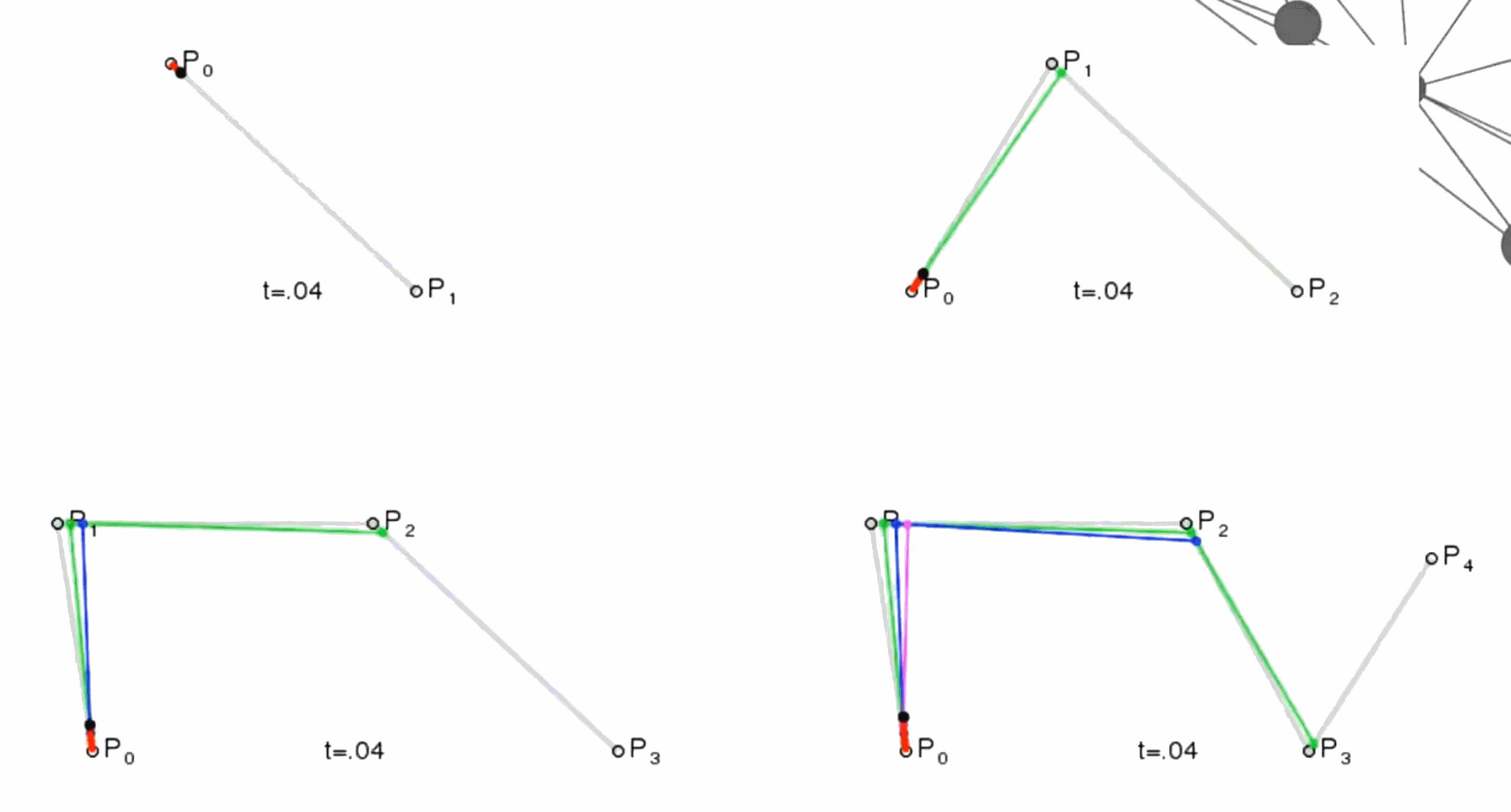
过起始点的B样条曲线

上述样条曲线在四点中间，并不过起始点，无法达到我们的拟合或者路径规划的任务

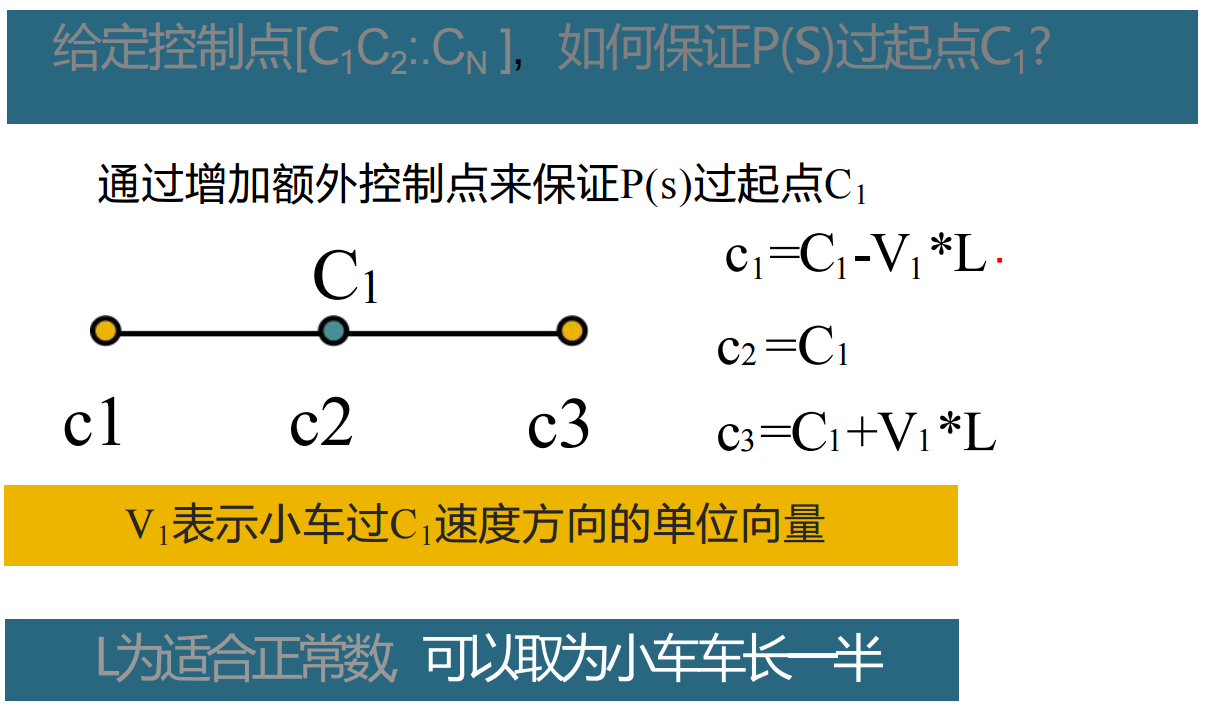
为了能够过起始点，我们采用在起始点添加对称的增广点：

但是采用这种增广模式，如何保证如何保证$P(S)$过起点$C_1$？

让我们算一算

上式也可以写成矩阵形式：

$$P(s)=\frac{1}{6} \begin{bmatrix} 1 & s & s^2 & s^3 \\ \end{bmatrix} \begin{bmatrix} 1 & 4 & 1 & 0 \\ -3 & 0 & 3 & 0 \\ 3 & -6 & 3 & 0 \\ -1 & 3 & -3 & 1 \end{bmatrix} \begin{bmatrix} C_1 \\ C_2 \\ C_3 \\ C_4 \\ \end{bmatrix}$$

根据矩阵乘法结合率可知：(AB)C=A(BC)

$$P(s)=\frac{1}{6} \begin{bmatrix} 1 & s & s^2 & s^3 \\ \end{bmatrix} \begin{bmatrix} C_1+4C_2+C_3 \\ -3C_1+3C_3 \\ 3C_1-6C_2+3C_3 \\ -C_1+3C_2-3C_3+C_4 \end{bmatrix}$$

根据起始点增广的形式我们可以得出：

\begin{align} C_{1}&=C_{O1}-V_1L \\ C_{2}&=C_{O1} \\ C_{3}&=C_{O1}+V_1L \end{align}

可以看出，这种定义使得原本的$C_1$（或$C_n$）在增广后的三点连线的中点，如下图所示

所以为了回答**”给定控制点[$C_1 \ C_2 \ ... \ C_N$]，如何保证$P(S)$过起点$C_1$？”**

我们可以将增广点代入上式，可得：

\begin{align} P(s)&=\frac{1}{6} \begin{bmatrix} 1 & s & s^2 & s^3 \\ \end{bmatrix} \begin{bmatrix} C_2+V_1L+4C_2+C_2-V_1L \\ -3C_2-3V_1L+3C_2-3V_1L \\ 3C_2+3V_1L-6C_2+3C_2-3V_1L \\ -C_2-V_1L+3C_2-3C_2+3V_1L+C_4 \end{bmatrix} \\ \\ &=\frac{1}{6} \begin{bmatrix} 1 & s & s^2 & s^3 \\ \end{bmatrix} \begin{bmatrix} 6C_2 \\ -6V_1L \\ 0 \\ -C_2+C_4+2V_1L \end{bmatrix} \\ \\ &= \begin{bmatrix} 1 & s & s^2 & s^3 \\ \end{bmatrix} \begin{bmatrix} C_2 \\ -V_1L \\ 0 \\ \frac{1}{6}(-C_2+C_4+2V_1L) \end{bmatrix} \end{align}

当$s=0$时，即在样条曲线起点：

$$P(0)=C_2$$

当我们重新在看这张图片时，就会恍然大悟了

当然，对于终点$C_N$,同理：

\begin{align} C_{N-2}&=C_{ON}-V_NL \\ C_{N-1}&=C_{ON} \\ C_{N} &=C_{ON}+V_NL \end{align}

代入增广矩阵方程：

$$P(s)=\frac{1}{6} \begin{bmatrix} 1 & s & s^2 & s^3 \\ \end{bmatrix} \begin{bmatrix} 1 & 4 & 1 & 0 \\ -3 & 0 & 3 & 0 \\ 3 & -6 & 3 & 0 \\ -1 & 3 & -3 & 1 \end{bmatrix} \begin{bmatrix} C_{N-3} \\ C_{N-2} \\ C_{N-1} \\ C_{N} \\ \end{bmatrix}$$

太复杂了，不想手算了 😦

根据MATLAB符号运算工具可知：

$$P(1)=C_{N-1}$$

即最后三点的中点，原始控制点的终点！

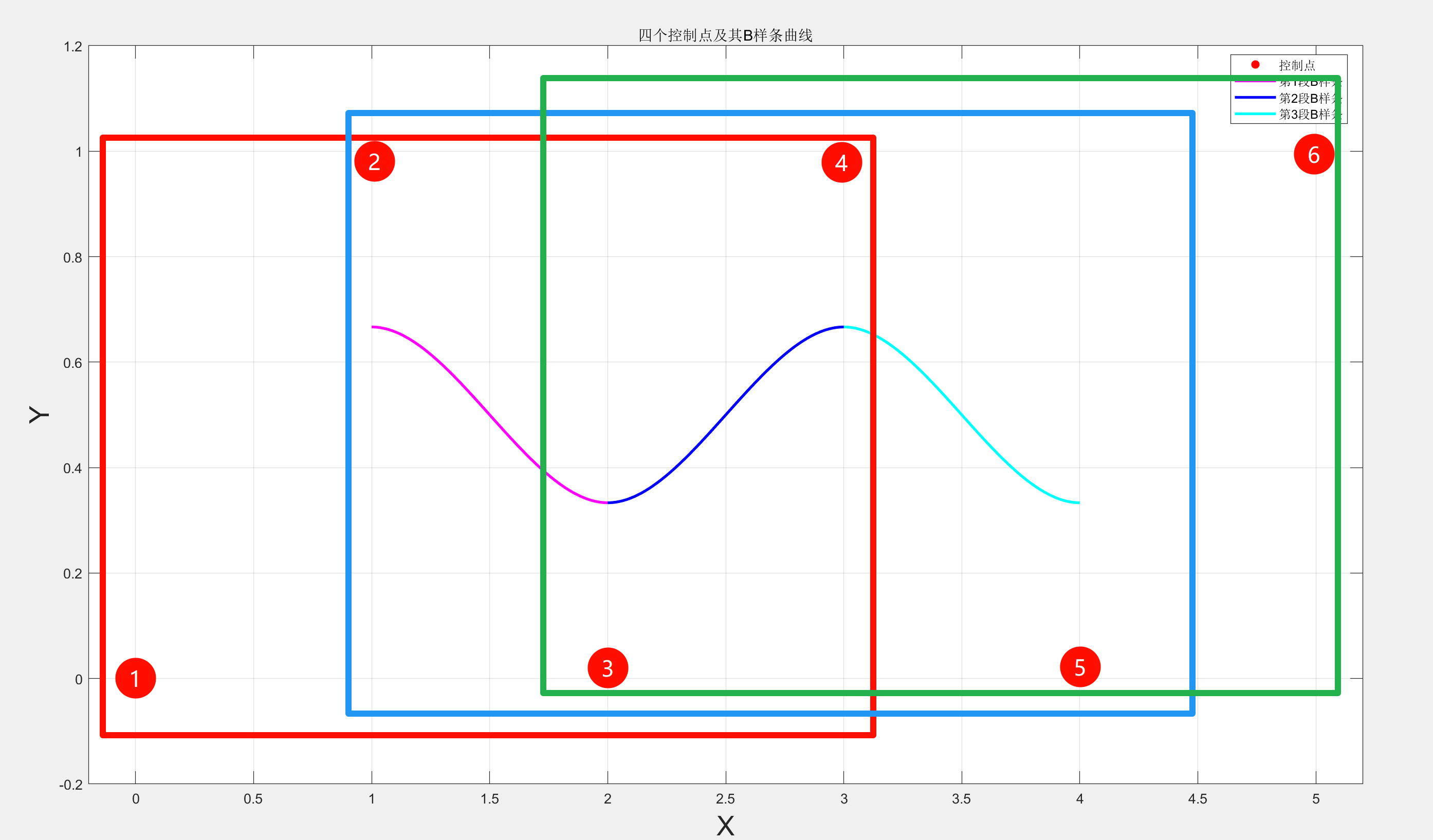
当然如果我们改变增广点的位置，使其不对称，就会出现以下情况：

对应图像变化：

是两点中点吗？

show me your code

当然我们可以通过MATLAB符号运算工具轻松得出任意增广点位的起始点和终点情况：

即：

$$P(0)=C_2-\frac{V_{11}L}{6}+\frac{V_{12}L}{6} \\ P(1)=C_{N-1}-\frac{V_{N1}L}{6}+\frac{V_{N2}L}{6} \\$$

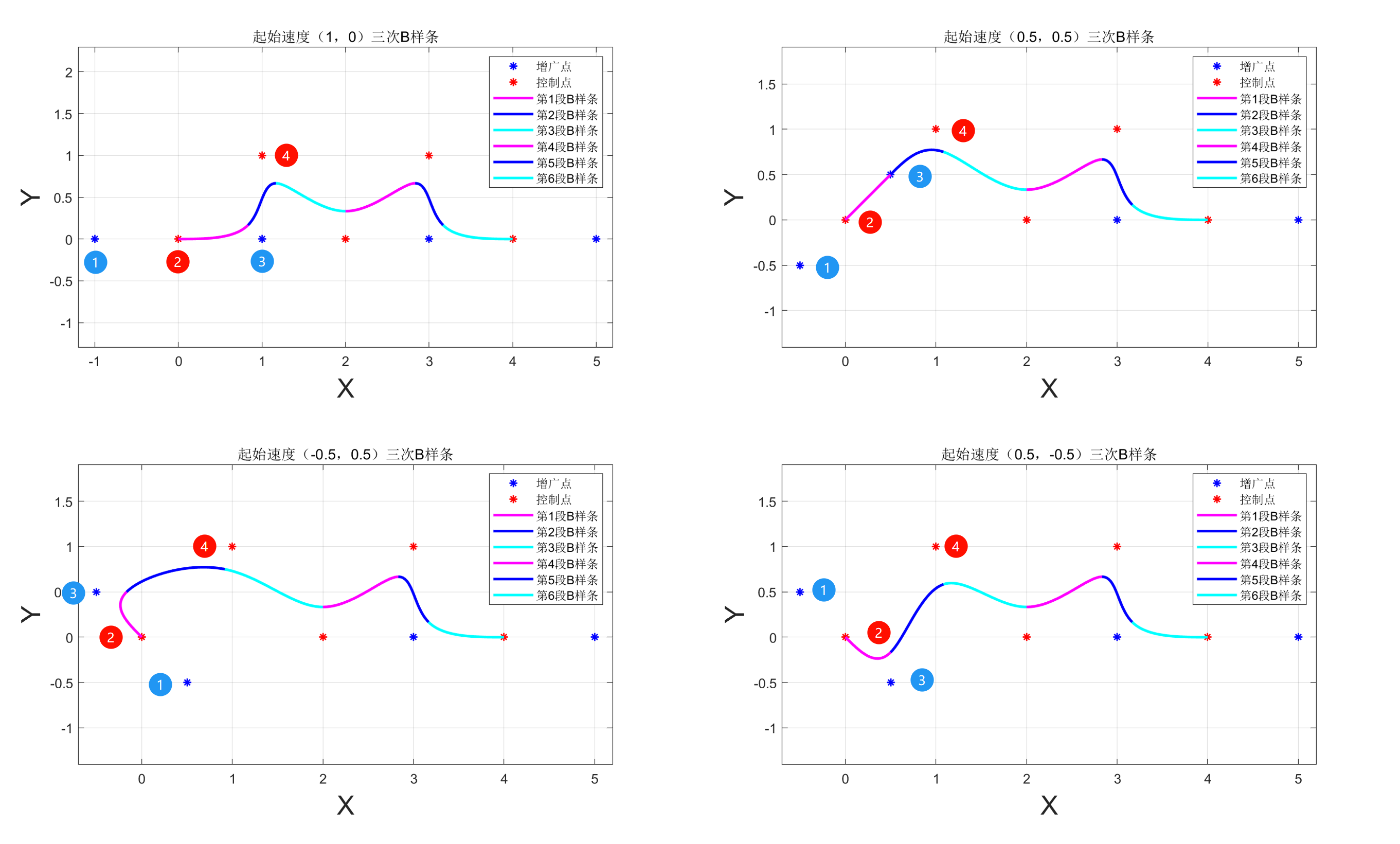
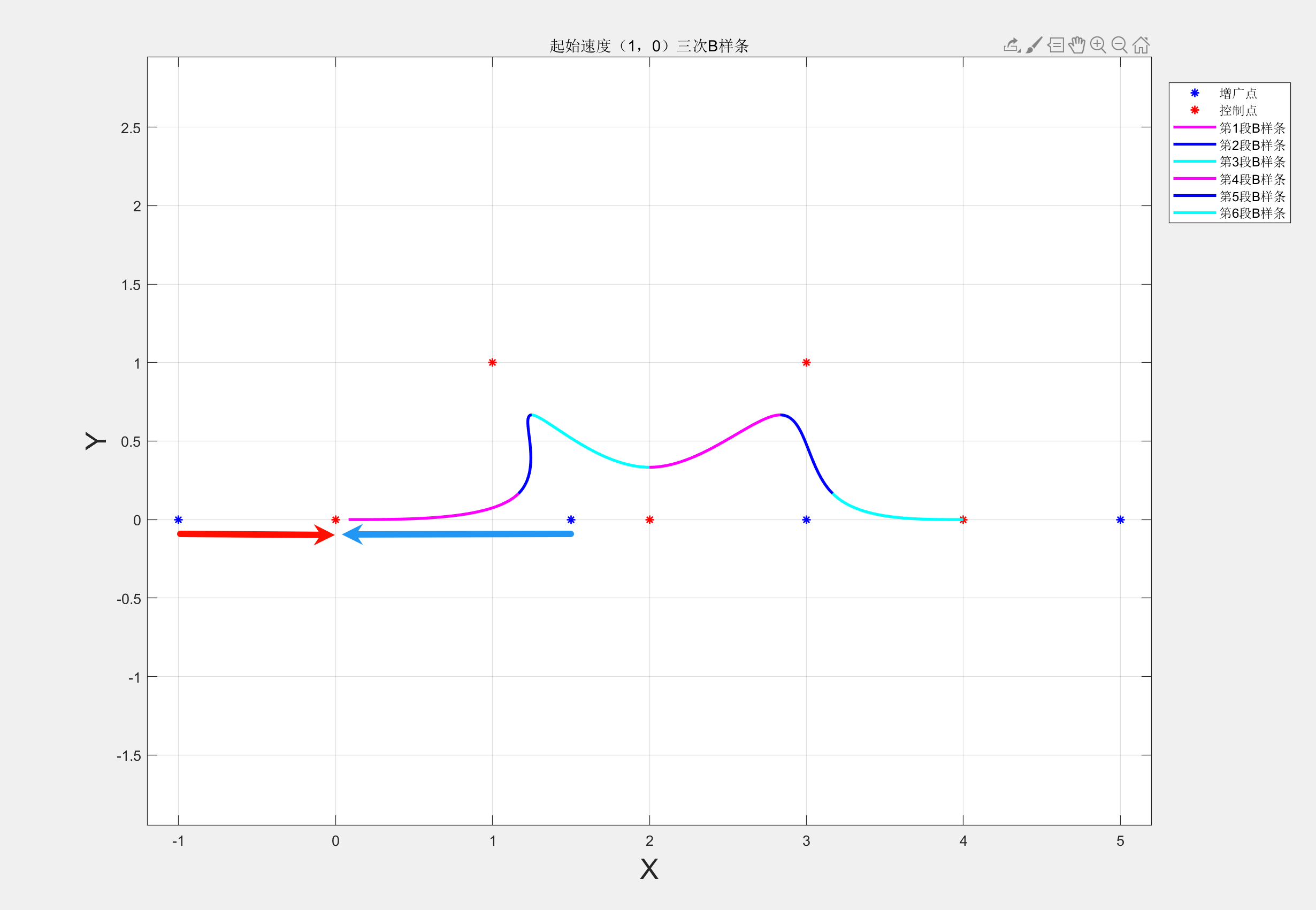
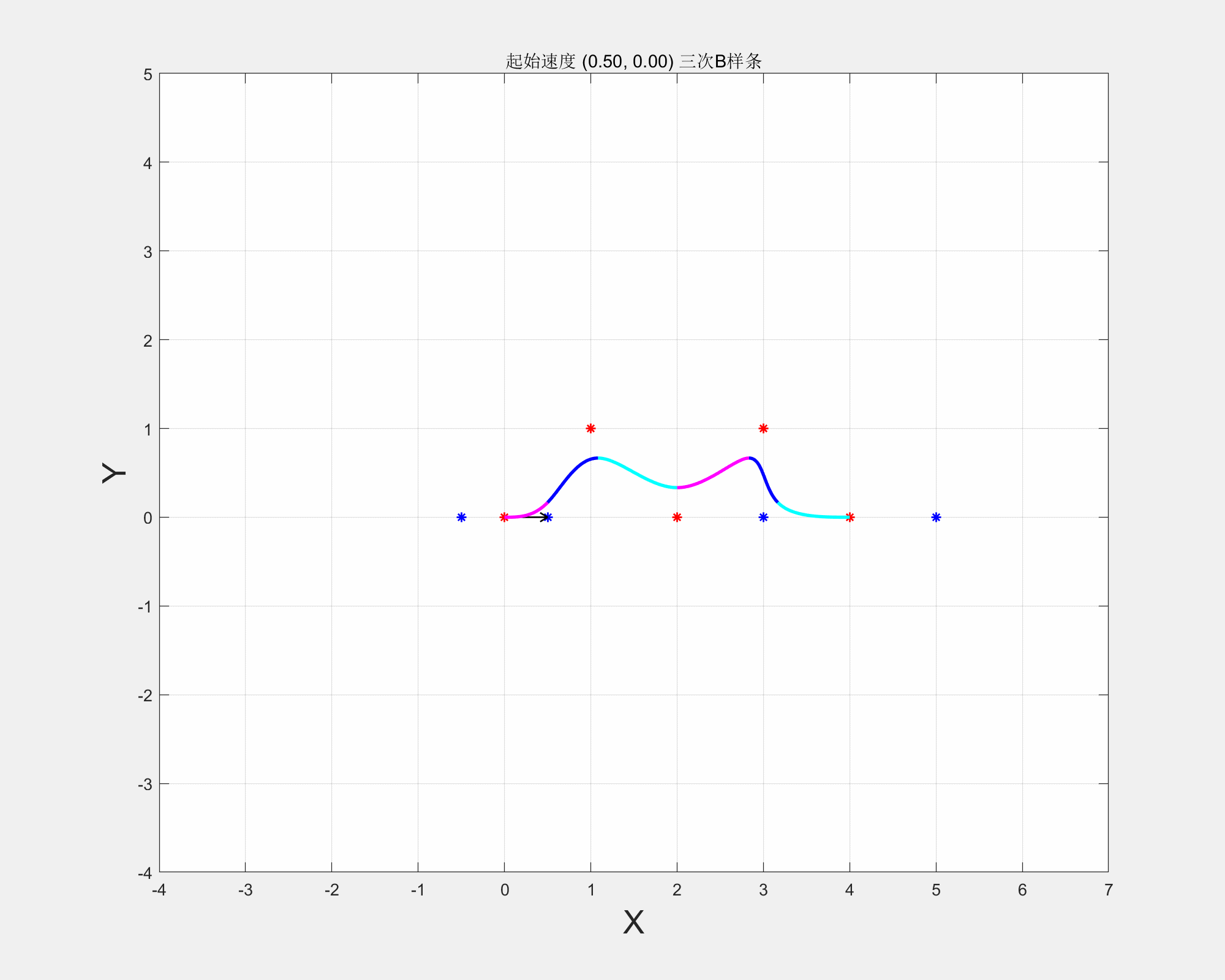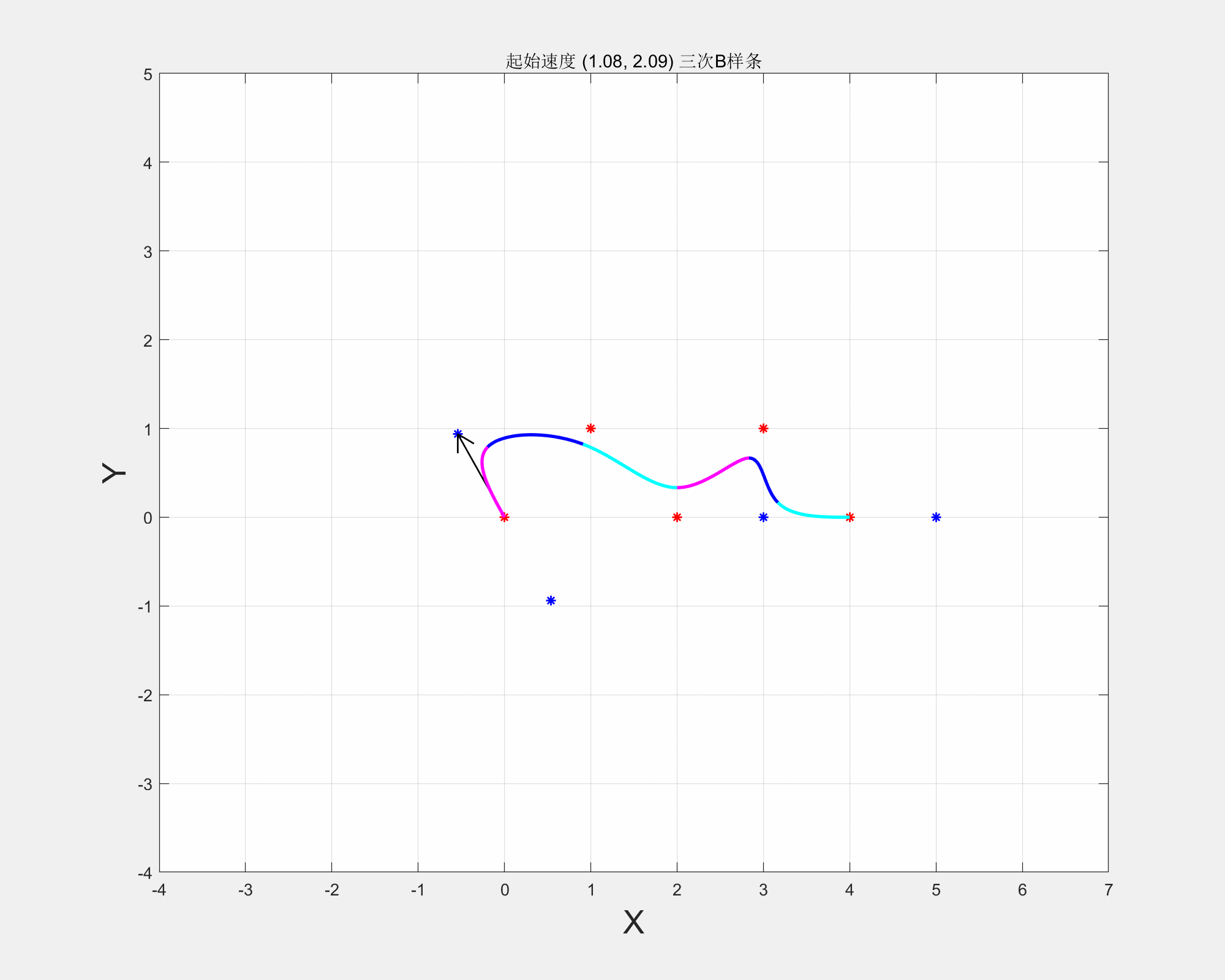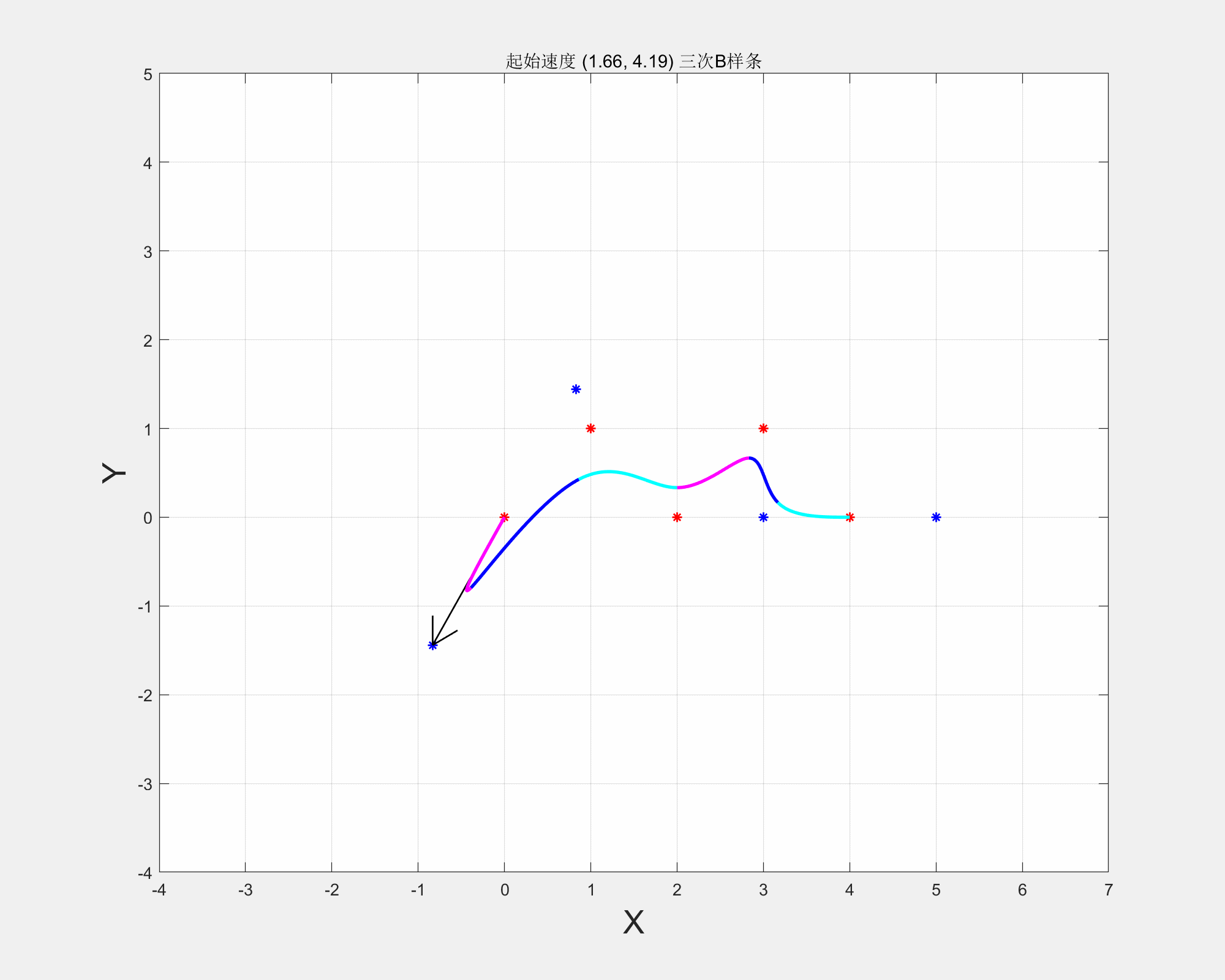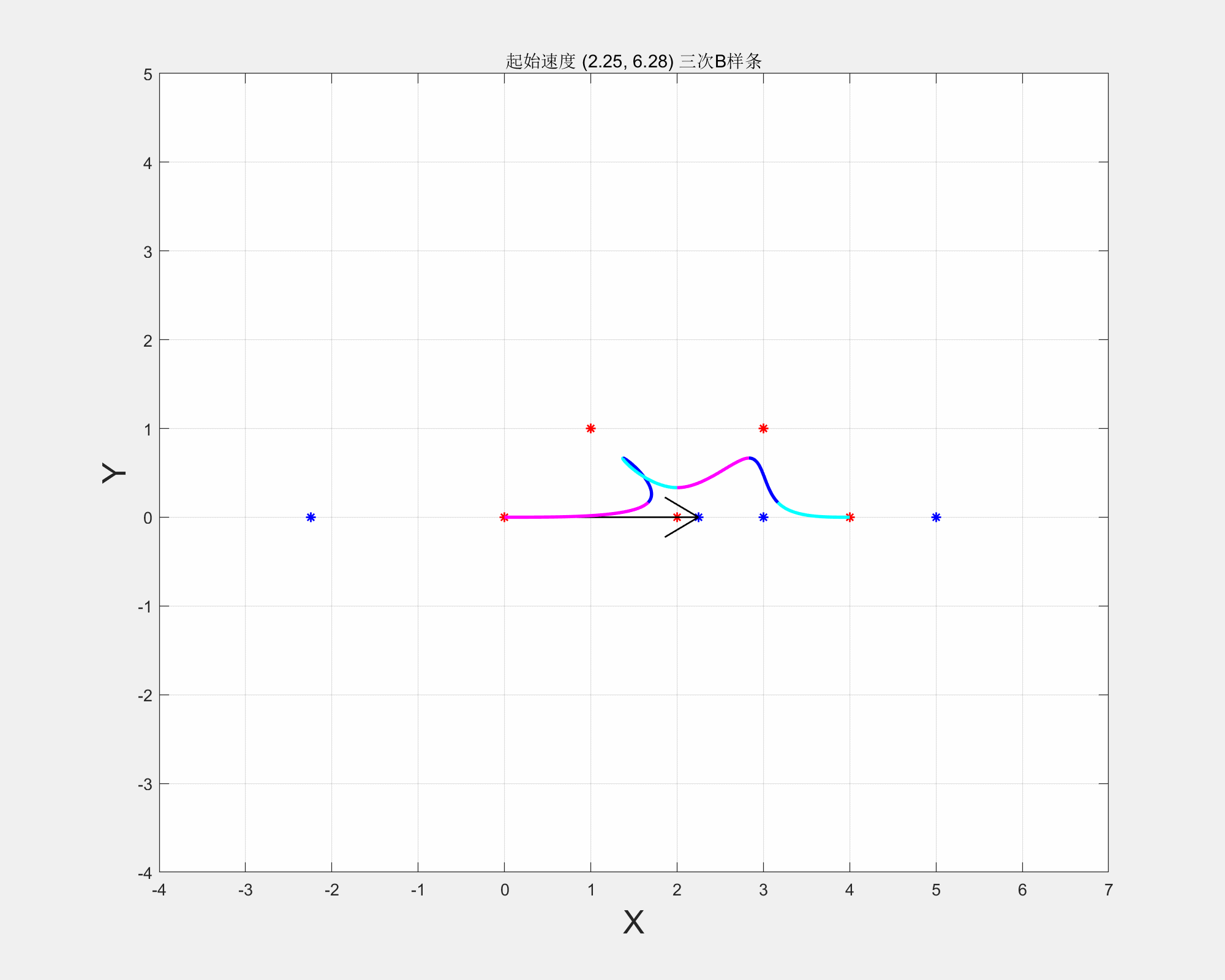
三次B样条在起始点速度对样条的影响

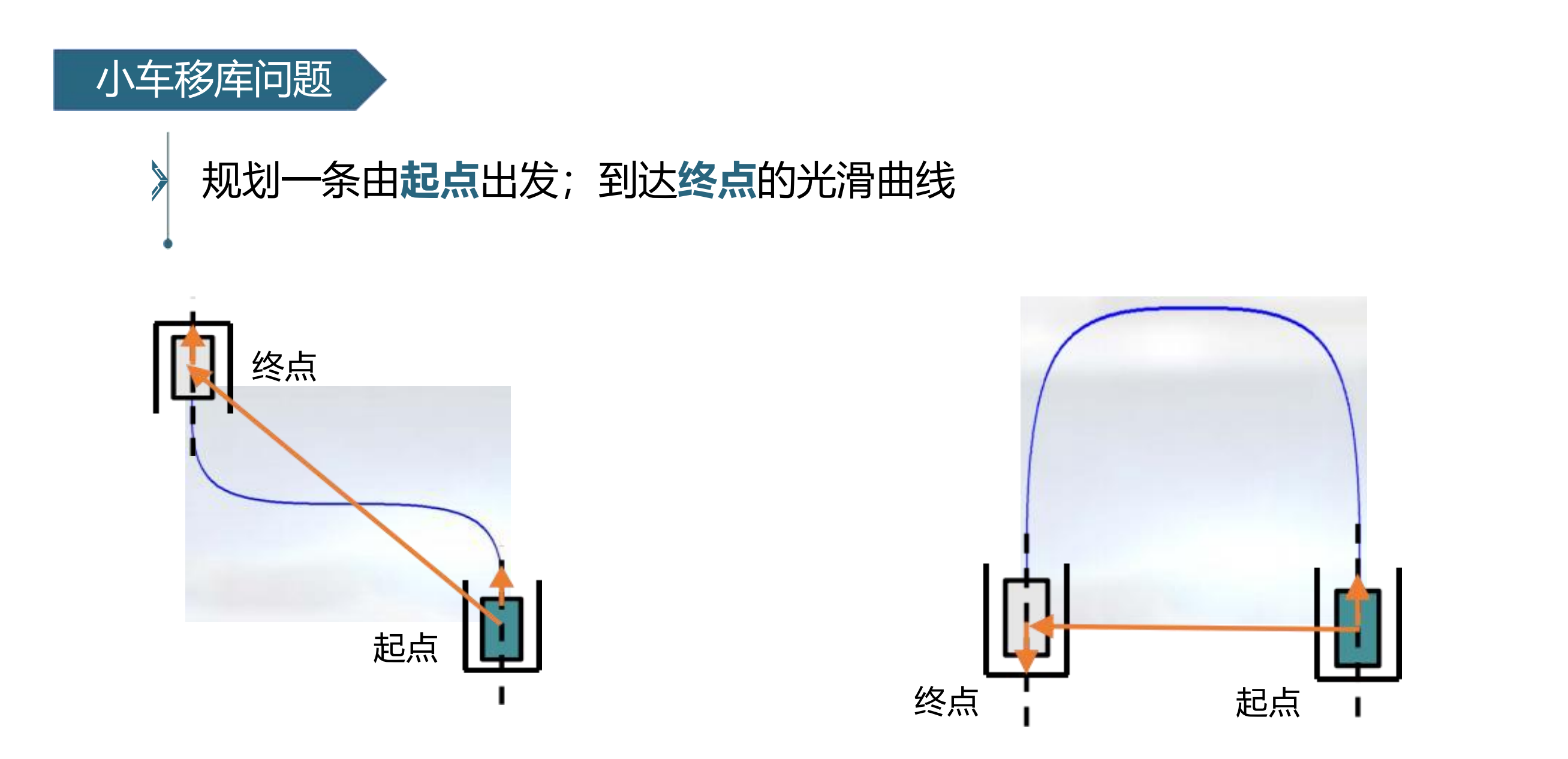
从应用角度：

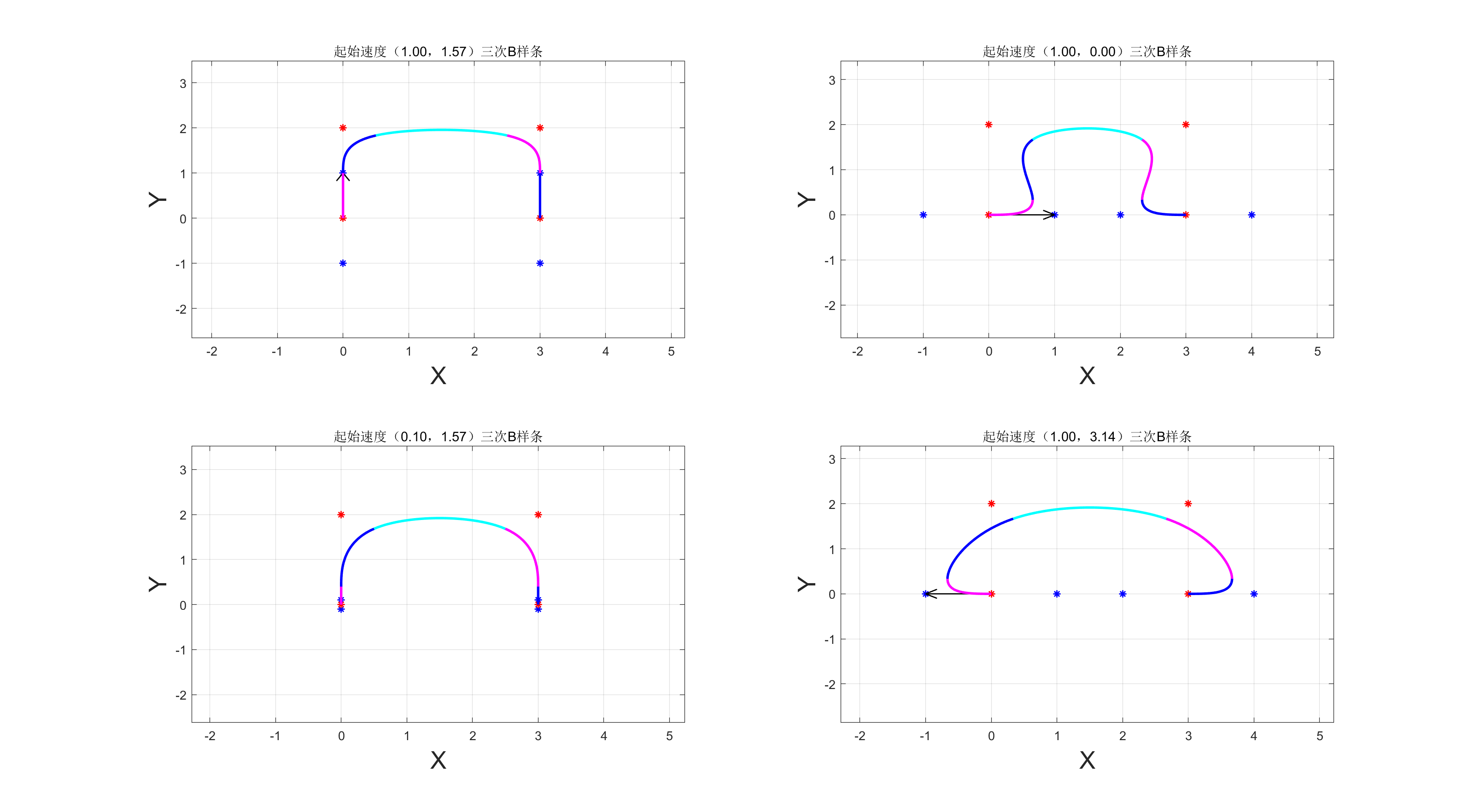
针对第二个入库问题，下列哪个是最合适的解法：

所以，起始点的速度$V$不同（方向和大小），最后生成的B样条也不同，最终方向取决于实际需求

许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章